Since my last blog on multivariate polynomial arithmetic, a lot has happened, so it's time to give an update, including our first parallel sparse multiplication benchmarks! In fact, there is so much to report that I'm restricting this blog to multiplication only!
The most exciting news since last time is that Daniel Schultz has gotten parallel sparse multiplication working. Daniel is the person we hired on the OpenDreamKit grant to work on parallel multivariate arithmetic. He's also implemented numerous improvements to the code, which I'll mention below.
After the last blog post, I discovered that a number of things affect the timings:
- Polynomial ordering (lex, deglex, degrevlex)
- Ordering of variables (x, y, z, t, u)
- Whether one computes f*g or g*f, or in the case of division, p/f or p/g
Obviously in a perfect system, none of these would matter, but especially with our old code and with certain systems, they do. In particular, some of the division timings I gave previously for Flint, were invalid. I've now corrected them on the old blog.
In this blog, I will give new timings which always force lex ordering, for x > y > z > t > u, and will always take f*g.
Sdmp and Maple prefer deglex, so I will time these separately. We also don't have them available on our benchmark machine anyway.
Magma, Sage and Singular support a virtual panoply of orderings, whilst some systems are restricted just to lex or just to deglex. Flint supports lex, deglex and degrevlex. (Since there is no agreement on what revlex should be, we decided not to support it.)
We also discovered that we had implemented degrevlex incorrectly, and this has now been fixed. This didn't affect the timings in the last blog.
Sage division improvements
In the last blog we noted that Sage performed much worse than Singular for division over Z. The Sage developers immediately took note of this and set about fixing it. The latest release is 8.0 and it doesn't seem to have the fix, so we have to wait for the new version to give the new Sage division timings. It's great to see how quickly the community responded to this.
It was of course fixed by using Singular for that computation, rather than a very slow generic implementation of division.
Singular improvements
Hans Schoenemann has been working on improving the use of Factory from Singular. This means that Singular will call Factory for large arithmetic operations, since it is much faster. Singular itself is optimised for Groebner basis computations, not arithmetic.
The new improvements will currently take effect for computations with over 1000 terms or so, which is heuristically chosen to avoid overhead in converting to and from Factory's lex ordering and recursive polynomial format. Changing from an arbitrary ordering to a lex ordering and back can be extremely expensive, so this crossover is essential to avoid harming performance for smaller operations.
We've also decided that when we have a really solid, performant implementation of multivariate arithmetic, we are going to make use of it in Factory. The end result is that the code that we are writing now will be available to all Singular (and Factory) users.
The main operations that really benefit from such arithmetic are rational functions and multivariate factorisation. They aren't for speeding up Groebner Basis computations!
Flint improvements
Most of the actual work done on Flint since my last blog, has been done by Daniel Schultz. Here are some of the improvements:
Improved exponent packing
When using deglex or degrevlex, our monomial format packs the total degree field into the same words as all the other exponent fields. The trick of packing exponent vectors into bit fields goes way back to the early days of Singular. We get the idea from a paper of Hans Schoenemann.
Actually, Singular keeps the degree field separate from the rest of the vector (which in hindsight might have been a better thing for us to do as well), but we decided to try and pack it along with the other exponents.
The problem with our implementation of deglex and degrevlex is precisely this extra field that is required for the degree. If we don't want to overflow a word for each exponent vector, we have fewer bits per exponent when using degree orderings.
The maximum total degree is also often larger than the maximum of any individual degree, further exacerbating the problem. These issues mean that if we aren't careful, we can take more space for packed monomials using degree orderings than for lex orderings.
In practice, this meant that for our largest benchmarks, two 64 bit words were being used for exponent vectors, instead of one. This is because we were packing each exponent into a 16 bit field. Obviously six times 16 bits requires more than 64 bits.
We were using 16 bit fields, since we only supported fields of 8, 16, 32 or 64 bits (including an overflow bit), and 8 bit fields just weren't large enough; the maximum total degree in our largest benchmark is 160, (which requires 8 bits, plus an overflow bit).
We now pack into an arbitrary number of bits, and for 5 variables plus a degree field, it obviously makes sense to pack into 10 bit fields, since you get 6 of those in 64 bits. This is plenty big enough for all our benchmarks, in fact. The result is a 50% saving in time when using degree orderings.
Delayed heap insertion
Recently at ISSAC 2017 here in Kaiserslautern, Roman Pearce, one of the authors of the Sdmp library, told me about an improvement for multiplication that delays inserting nodes into the heap. In some cases, we know that they will be inserted at a later time anyway, so there is no hurry to put them in at the earliest possible opportunity, as this just increases the size of the heap.
Daniel implemented a version of this that he came up with, and it makes a big difference in timings, and shrinks the heap to a fraction of its original size.
Multi-core multiplication
Flint can now multiply sparse multivariate polynomials using threads. Daniel experimented with various strategies, including breaking one of the polynomials up. This strategy has the disadvantage of requiring a merge of polynomials from the various threads at the end, which is expensive.
The best strategy we found was to take "diagonals". That is, we divide the output polynomial up into chunks instead of dividing up the input polynomials. This has to be done heuristically, of course, since you don't have the output polynomial until it is computed.
This idea is contained in a paper of Jacques Laskar and Mickael Gastineau.
To ensure that all threads take about the same amount of time, we start with big blocks and take smaller and smaller blocks towards the end, so that no thread will be left running for a long time at the end while all the others are waiting. This gives fairly regular performance. The scheme we use is a variation on that found in the paper by Laskar and Gastineau.
The advantage of the diagonal splitting method is that no merge is required at the end of the computation. One simply needs to concatenate the various outputs from the threads, and this can be done relatively efficiently.
Improved memory allocation
At scale, everything breaks, and malloc and the Flint memory manager are no exception. I wrote a new memory manager for Flint which uses thread local storage to manage allocations in a way that tries to prevent different threads writing to adjacent memory locations (which would incur a performance penalty).
The design of this memory manager is beyond the scope of this blog, but it seems to work in practice.
[A brief summary is that it allocates blocks of memory per thread, consisting of a few pages each. Each page has a header which points to the header of the first page in the block, where a count of the number of active allocations is stored. When this count reaches zero, the entire block is deleted. When threads terminate, blocks are marked as moribund so that further allocations are not made in them. The main thread can still clean thread allocated blocks up when their count reaches zero, but no further allocations are made in those blocks.]
The main advantage of this scheme, apart from keeping memory separated between threads is that we can block-allocate the mpz_t's that are used for the polynomial coefficients. This is critical, since in our largest benchmarks, almost a third of the time is spent allocating space for the output!
Unfortunately, each mpz_t allocates a small block of memory internally. That memory is handled by GMP/MPIR, not Flint, and so we still have 28 million small allocations for our largest benchmark!
I was able to make a small improvement here by changing the default allocation to two words, since we don't really use one word GMP integers in Flint anyway. But fundamentally, we are still making many small allocations at this point, which is very expensive.
This can be improved in a future version of Flint by setting a custom GMP memory allocator. But it will require implementation of a threaded, pooled, bump allocator. It can be done, but it will be a lot of work.
If we want to scale up to more than 4 cores (and we do!), we have no choice but to fix this!
Trip homogeneous format
Mickael Gastineau, one of the authors of Trip, was kind enough to send me a special version of Trip which allows access to their homogeneous polynomial format. It isn't optimised for integer arithmetic, but their papers show it is very fast for dense multivariate arithmetic, assuming you are happy to wait for a long precomputation.
The basic idea is to split polynomials into homogeneous components and precompute a very large table in memory for lookup. One only needs a table for the given degree bound, and Trip manages this automatically upon encountering this degree for the first time.
Before we get to the main timings below, we present Trip timings with this homogeneous format (excluding the precomputation).
We only time this for dense computations, since the precomputation is not practical for most of the sparse benchmarks. Moreover, since the code is not optimised for integer arithmetic, we use floating point to exactly represent integers, which means that the largest benchmarks can't be performed, since they would overflow the double precision floating point numbers.
Since Flint doesn't yet have parallel dense multiplication, these timings are restricted to a single core.
Dense Fateman (1 core)
New sparse multiplication benchmarks
In this section, we give timings for all systems (except Sdmp and Maple) on 1, 2 and 4 cores (where available). Most of the systems, including ours, perform badly on larger numbers of cores, unless the problems are really huge (> 30 minutes to run). When we have fixed our memory management issues, we'll do another blog post with timings on larger numbers of cores.
All the systems below were forced to use lexicographical ordering, with x > y > z > t > u, and we always take f*g (the polynomials f and g are the same length, so it's an arbitrary choice in reality).
The new delayed insertion technique Daniel implemented actually makes the timings for f*g and g*f the same for our new code. But other systems that support lex don't necessarily have this.
All of the timings in this section are done on the same machine, an old 2.2GHz Opteron server.
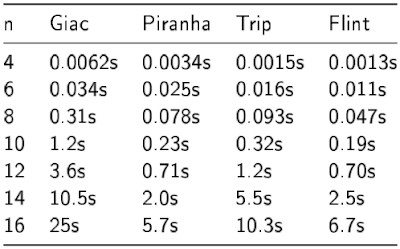
First, we give all the single core timings. We've added Piranha and Trip timings this time around. Incidentally, my understanding is that Piranha uses a hash table and therefore doesn't have a specific polynomial ordering. We include timings for Piranha to quench your burning curiosity.
Dense Fateman (1 core)
Sparse Pearce (1 core)
Of course, not all the systems can do parallel multiplication. So a smaller set of benchmarks for a smaller set of systems follows.
Sparse Pearce (2 core)
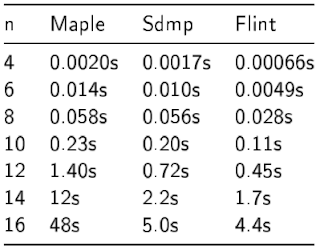
Sdmp and Maple 2017 timings
Michael Monagan very kindly granted me guest access to a machine that has Maple 2017 installed, which is currently also the only way to time Sdmp. Roman Pearce has also kindly given lots of information on how to use Maple and Sdmp, so that we can get fair timings.
The first thing to note is that the timings here are on a completely different machine to the above. So they are not in any way comparable.
I believe Sdmp internally only supports deglex. Therefore, we decided it best to use deglex for the Maple and Sdmp timings, otherwise we may be comparing apples and oranges. This is another reason one can't make a direct comparison with the timings for the other systems above. It also means there are no dense benchmarks, since our dense code doesn't support deglex efficiently yet.
It's also very important to point out that we have no way to run Sdmp except via Maple. We don't always get the timings for Sdmp below in practice, they are simply the self-reported times for Sdmp as a component of the full Maple run times.
It's not entirely clear why Maple is so slow on large inputs. Maple makes use of a DAG structure for its symbolic engine, rather than directly manipulating Sdmp polynomials. Something is apparently causing this to be incredibly slow when the polynomials are large. According to the Maple CodeTools it seems to be doing some long garbage collection runs after each multiplication. One wonders if there isn't something better that Maple can do so that their users can take practical advantage of the full performance of the Sdmp library in all cases!
An important benchmarking consideration is that for Maple, all Sdmp computations can be considered static. This means that Sdmp can block allocate their outputs, since the coefficients will never be mutated and therefore will never be reallocated. To simulate this, when comparing Sdmp and Flint, we write Flint polynomials into an already allocated polynomial. This probably slightly advantages Flint in some cases, but since we don't actually get the stated Sdmp timings in practice, this seems reasonable.
Of course, this isn't fair to Maple, but we are talking about a few percent, and the comparison with Sdmp was more interesting to us, since it is a library like Flint.
When comparing against Maple, we do the Flint timings using Nemo, which is a Julia package that wraps Flint. The code isn't on by default in Nemo, since we don't yet have GCD code, for example, but we switch the Flint code on in Nemo for the basic arithmetic timings in this blog.
We take considerable care to ensure that both Maple and Sdmp use the same effective variable order that we do.
Sparse Pearce (1 core)
Sparse Pearce (4 core)
Conclusion
The project is coming along nicely.
Daniel has started working on arithmetic over Q, and we'll update everyone when that is working. Hopefully we'll also find a good strategy for parallelisation of dense multiplication.
I should point out that the code described in this blog is very new, and after the last blog, we found many things that changed the results. We've taken much more care this time, but even an infinite amount of effort won't avoid all possible sources of error. The code itself is merged into trunk, since we mostly trust it, but it should still be considered experimental until it settles a bit.
I wish to thank Roman Pearce, Michael Monagan and Mickael Gastineau who have very generously provided details of how to use their systems, and gave us access so that we could do timings. There is an academic version of Trip available, which has everything but the homogeneous algorithm. For that, Mickael prepared a special version we could make use of.
We also want to thank the EU for their Horizon 2020 funding of the OpenDreamKit project.